|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| DUYURULAR |
|
|
|
|
|
|
|
|
|
|
|
|
 |
AÇISAL FONKSİYONLAR |
|
01.06.2020
|
AÇISAL FONKSiYONUN ÜÇGENLERDEKi HESABI
|
|
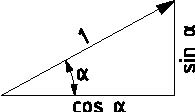
BiR AÇIDA FONKSiYONLARIN KARŞILIKLI DURUMU
|
|
|
PİSAGOR’A GÖRE
sin2 + cos2 = 1
|
Karşı Kenar
Tan α = -------------------
Yan dik kenar
sin α
tan α = ------------
cos α
|
Yan dik kenar
cota = -----------------
Karşı dik kenar
cos α
cot α= ----------
sin α
|
tan α . cot α = 1
|
|
sin(α±β) =sin α . cos β ± cos α . sin β cos(α±β) = cos α . cos β m sin α . sin β
tan α ± tan β cot α . cot β ± 1
tan (α±β) = ------------------- cot (α±β) = -----------------------
1 m tan α . tan β cot α ± cot β
|
|
2 . tanα
tan2α= 2 . sinα . cosα tan2α= ------------------
1−tan2 α
cot2 α−1
cos2α=cos2 α−sin2 α cos2α= -----------------
2 . cot α
|
1
sinα= √ ----- (1−cos 2α ) cosα±sinα= √ 1±sin2α
2
1 1−cos 2α
cosα= √ ------- (1+cos2α ) tanα= √ -----------------
2 1+cos 2α
3
|
|
ÖNEMLİ AÇISAL FONKSİYONLAR
|
|
|
0°
|
30°
|
45°
|
60°
|
90°
|
|
0°
|
30°
|
45°
|
60°
|
90°
|
|
sin
|
0
|
1/2 =0,5
|
1/2 √2 =0,707
|
1/2√3 =0,866
|
1
|
tan
|
0
|
1/3√3 =0,577
|
1
|
√3 =1,732
|
∞
|
|
cos
|
1
|
1/2√ 3 =0,866
|
1/ 2√ 2 =0,707
|
1/2 =0,5
|
0
|
cot
|
∞
|
√3 =1,732
|
1
|
1/3 √3 =0,577
|
0
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
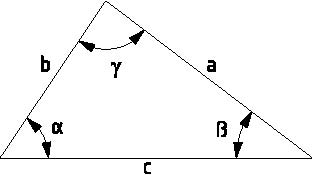
GENİŞ AÇILI ÜÇGENLERDE AÇISAL FONKSİYONLAR
|
|
|
|
|
SİNÜS DEĞERİ
|
KOSİNÜS DEĞERİ
|
|
a : b : c = sin α : sin β: sin γ
|
a2 = b2 + c2 — 2bc . cosα
|
|
a sinα = b sinβ = c sinγ
|
b2 = a2 + c2 — 2ac . cosβ
|
|
c2 = a2 + b2 — 2ab . cosγ
|
|
|
|
|
|
SİNÜS VE KOSİNÜSÜN KULLANIMI
|
|
KENAR HESABI
|
AÇI HESABI
|
YÜZEY HESABI
|
|
a = b . sinα sinβ = c . sinα sinγ
|
sinα= a . sinβ b = a . sin γ c
|
cosα=b2 +c2 −a2 2bc
|
A = a . b . sinγ 2
|
|
b = a . sinβ sinα = c . sinβ sinγ
|
sinβ=b . sinα a = b . sin γ c
|
cosβ= a2 +c2 +b2 2ac
|
A = b . c . sinα 2
|
|
c = a . sinα sinα = b . sinγ sinβ
|
sinγ=c . sinα a = c . sinβ b
|
cos γ=a2 +b2 −c2 2ab
|
A = a . c . sinβ 2
|
|
|
|
AÇISINA GÖRE KENAR FONKSİYONLARI HESABI cosβ= b c . cosβ= a c . tanβ= b a . cotβ= a b
|
|
|
a =c.sinα =b . tanα = b cotα
|
b =c.sinα = a tanα =a . cotα
|
c = a sinα = b cosα
|
a =c . cosβ = b tanβ =b . cotβ
|
b =c . sinβ =a . tanβ = a cotα
|
c = b sinβ = a cosβ
|
| |
|
|
|
|
|
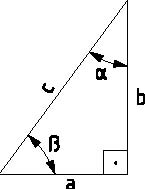
TRİGONOMETRİ
|
|
Karşı Kenar a
Sin α = ---------------------- = ------ Hipotenüs c
|
Karşı Dik Kenar a
Tg α = ------------------------ = -------
Yan Dik Kenar b
|
|
kenar Kenar b
Cos α= ---------------------- = ------
Hipotenüs c
|
Yan dik kenar b
Cotg α = --------------------- = -------
Karşı Dik Kenar a
|
AÇILARIN TRİGONOMETRİK FONKSİYONLARI
|
DERECE
|
0
|
30°
|
45°
|
60°
|
90°
|
180°
|
270°
|
360°
|
|
Sin
|
0
|
0,5
|
0,707
|
0,866
|
1
|
0
|
—1
|
0
|
|
Cos
|
1
|
0,866
|
0,707
|
0,5
|
0
|
—1
|
0
|
1
|
|
tg
|
0
|
0,577
|
1
|
1,732
|
∞
|
0
|
∞
|
0
|
|
Cotg
|
∞
|
1,732
|
1
|
0,577
|
0
|
∞
|
0
|
∞
|
|
YUNAN (GREEK) ALFABESİ
|
|
alfa
|
A
|
α
|
A
|
α
|
nu
|
N
|
γ
|
N
|
γ
|
|
beta
|
B
|
β
|
B
|
β
|
ksi
|
E
|
ε
|
E
|
ε
|
|
gama
|
r
|
γ
|
r
|
γ
|
omikron
|
O
|
ο
|
O
|
ο
|
|
delta
|
Δ
|
δ
|
Δ
|
δ
|
pi
|
π
|
πϖ
|
π
|
πϖ
|
|
epsilon
|
E
|
ε, ε
|
E
|
ε, ε
|
ro
|
P
|
ρ
|
P
|
ρ
|
|
zeta
|
Z
|
ζ
|
Z
|
ζ
|
sigma
|
Σ
|
σ
|
Σ
|
σ
|
|
eta
|
H
|
η
|
H
|
η
|
tau
|
T
|
τ
|
T
|
τ
|
|
teta
|
θ
|
ν,θ
|
θ
|
ν,θ
|
upsilon
|
ϒ
|
ν
|
ϒ
|
ν
|
|
ita
|
l
|
ι
|
l
|
ι
|
fi
|
Φ
|
Φ, Φ
|
Φ
|
Φ, Φ
|
|
kaba
|
K
|
χ, κ
|
K
|
χ, κ
|
ki
|
X
|
χ
|
X
|
χ
|
|
lamda
|
λ
|
λ
|
λ
|
λ
|
psi
|
Ψ
|
Ψ
|
Ψ
|
Ψ
|
|
znu
|
M
|
µ
|
M
|
µ
|
omega
|
Ω
|
ω
|
Ω
|
ω
|
(n) DEĞERİNİN ÜST KATLARI
(n) DEĞERİNİN ALT KATLARI
|
Exa
|
(E)
|
=
|
1018
|
=
|
1.000.000.000.000.000.000
|
|
Peta
|
(P)
|
=
|
1015
|
=
|
1.000.000.000.000.000
|
|
Tera
|
(T)
|
=
|
1012
|
=
|
1.000.000.000.000
|
|
Giga
|
(G)
|
=
|
109
|
=
|
1.000.000.000
|
|
Mega
|
(M)
|
=
|
106
|
=
|
1.000.000
|
|
Kilo
|
(K)
|
=
|
103
|
=
|
1.000
|
|
Hekto
|
(h)
|
=
|
102
|
=
|
100
|
|
Deka
|
(D)
|
=
|
101
|
=
|
10
|
|
Dezi
|
(d) =
|
10—1
|
=
|
0,1
|
|
Zenti
|
(c) =
|
10—2
|
=
|
0,01
|
|
Mili
|
(m) =
|
10—3
|
=
|
0,001
|
|
Mikro
|
(Μ)=
|
10—6
|
=
|
0,000.001
|
|
Nano
|
(n) =
|
10—9
|
=
|
0,000.000.001
|
|
Pico
|
(p) =
|
10—12
|
=
|
0,000.000.000.001
|
|
Femto
|
(f) =
|
10—15
|
=
|
0.000.000.000.000.001
|
|
Atto
|
(a) =
|
10—18
|
=
|
0.000.000.000.000.000.001
|
www.kar-el.com.tr
AÇIKLAMA: radyan derece dönüşümü, derece radyan grad, radyan bulma, radyan nasıl bulunur, radyan hesaplama formülü, 1 derece kaç mm dir, 1 devir kaç radyan, devir/dakika metre/saniye, trigonometrik fonksiyonlar 11. sınıf, Trigonometrik fonksiyonlar Formülleri, Trigonometrik Fonksiyonlar SIRALAMA, Trigonometrik fonksiyonlar değerleri, TRİGONOMETRİK FONKSİYONLAR 11. Sınıf Soru ve çözümleri, Trigonometrik fonksiyonlar nedir, Trigonometrik fonksiyonlar Türevi, Trigonometrik Fonksiyonlar PDF, Trigonometrik Fonksiyonlar üniversite, Trigonometrik Fonksiyonlar Grafikleri, Trigonometrik formüller, Trigonometrik fonksiyonlar formüller
FİRMAMIZ ; Pisagor, sinus degeri, kosinüs degeri
GÜNCEL TESİSAT MALZEME FİYATLARI ANKARA
ANKARA’DA SIHHİ TESİSAT, ANKARA’DA KALÖRİFER TESİSATI MALZEMELERİ, ANKARA’DA DOGALGAZ
TESİSAT MALZEMELERİ,GÜNCEL FİYATLAR
KAR-EL İNŞAAT VE TESİSAT MALZEMELERİ LTD ŞTİ. ULUS- MERKEZ : 0312 311 24 44 TİMKO-ŞUBE : 0312 354 34 35
|
|